Linear, Polinomial dan Eksponensial

Kembali ke Halaman Awal

Consider the three functions $y=x$ , $y=x^4$ and $y=2^x$ .

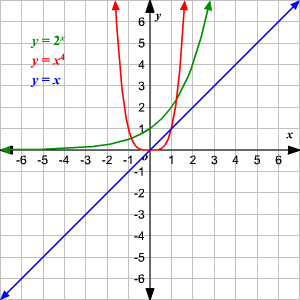
The first is a linear function ; its graph is a straight line.

The second is a polynomial function .

The third is an exponential function .

Suppose you graph all three on the same axes, and ask the question, “Which function grows the fastest for large values of $x$ ?”

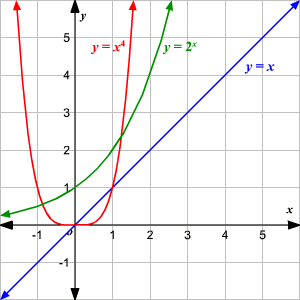
In this graph, it appears that the answer is $y=x^4$ . It is greater than $y=2^x$ for all values shown.

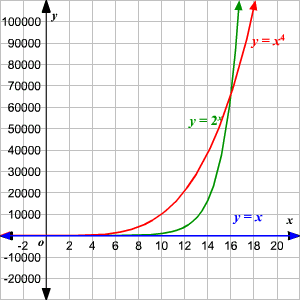
However, if we zoom out the $y$ -axis quite a lot, we see that at $x=16$ , $y=2^x$ overtakes $y=x^4$ , and after this point, $y=2^x$ grows faster. (Note that with the axes scaled this way, $y=x$ grows so slowly

that it is indistinguishable from the $x$ -axis.)

In fact, it can be shown that this is true for ANY exponential function and ANY polynomial function with positive growth. The exponential function will eventually outstrip the polynomial function.

Kembali ke Halaman Awal